The solution to the Newtonian equation give the well known conics
where 
and e is the eccentricity of the orbit
[ if e=0 it is circular ].
We can obtain an approximate solution 
to the exact orbit equation
[ valid for 
], if we substitute the Newtonian
solution into the term quadratic in U, that is if we solve
where we have put 
[ for timelike orbits ]. This
equation is solved by choosing a particular integral of the
form [ Assignment 7 ]:
This gives
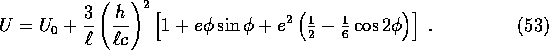
The most important term is the one that is linear in 
because it is the only one which in the course of time [ with many
revolutions of the planet ] becomes larger and larger. We therefore
ignore the other corrections to 
and obtain
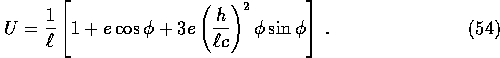
Now
But we have 
so 
,
and this simplifies our solution to
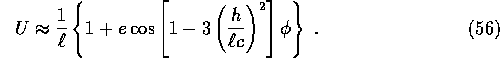
The orbit of the planet is thus only approximately an ellipse.
The solution for U is still a periodic function, but
no longer with a period 
. The point at which the
orbit is closest to the sun is reached again only after
an additional rotation through the angle
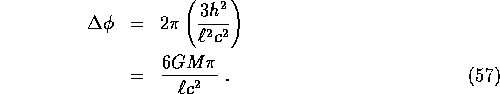
This is the famous perihelion precession
of planetary orbits. For Mercury we obtain 43.03'' per century.